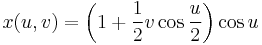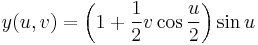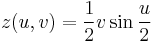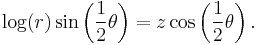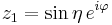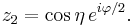Möbius strip
The Möbius strip or Möbius band (pronounced UK: /ˈmɜːbiəs/ or US: /ˈmoʊbiəs/ in English, [ˈmøːbi̯ʊs] in German) (alternatively written Mobius or Moebius in English) is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface. It was discovered independently by the German mathematicians August Ferdinand Möbius and Johann Benedict Listing in 1858.[1][2][3]
A model can easily be created by taking a paper strip and giving it a half-twist, and then joining the ends of the strip together to form a loop. In Euclidean space there are in fact two types of Möbius strips depending on the direction of the half-twist: clockwise and counterclockwise. That is to say, it is a chiral object with "handedness" (right-handed or left-handed).
It is straightforward to find algebraic equations the solutions of which have the topology of a Möbius strip, but in general these equations do not describe the same geometric shape that one gets from the twisted paper model described above. In particular, the twisted paper model is a developable surface (it has zero Gaussian curvature). A system of differential-algebraic equations that describes models of this type was published in 2007 together with its numerical solution.[4]
The Euler characteristic of the Möbius strip is zero.
Contents |
Properties
The Möbius strip has several curious properties. A line drawn starting from the seam down the middle will meet back at the seam but at the "other side". If continued the line will meet the starting point and will be double the length of the original strip. This single continuous curve demonstrates that the Möbius strip has only one boundary.
Cutting a Möbius strip along the center line yields one long strip with two full twists in it, rather than two separate strips; the result is not a Möbius strip. This happens because the original strip only has one edge that is twice as long as the original strip. Cutting creates a second independent edge, half of which was on each side of the scissors. Cutting this new, longer, strip down the middle creates two strips wound around each other, each with two full twists.
If the strip is cut along about a third of the way in from the edge, it creates two strips: One is a thinner Möbius strip — it is the center third of the original strip, comprising 1/3 of the width and the same length as the original strip. The other is a longer but thin strip with two full twists in it — this is a neighborhood of the edge of the original strip, and it comprises 1/3 of the width and twice the length of the original strip.
Other analogous strips can be obtained by similarly joining strips with two or more half-twists in them instead of one. For example, a strip with three half-twists, when divided lengthwise, becomes a strip tied in a trefoil knot. (If this knot is unravelled, the strip is made with eight half-twists in addition to an overhand knot.) The equation for the number of half-twists after cutting a Mobius strip is 2N+2=M, where N is the number of half-twists before and M, the number after cutting a Möbius strip, giving it extra twists, and reconnecting the ends produces figures called paradromic rings.
A strip with an odd-number of half-twists, such as the Möbius strip, will have only one surface and one boundary. A strip twisted an even number of times will have two surfaces and two boundaries.
If a strip with an odd number of half-twists is cut in half along its length, it will result in a longer strip, with the same number of loops as there are half-twists in the original. Alternatively, if a strip with an even number of half-twists is cut in half along its length, it will result in two conjoined strips, each with the same number of twists as the original.
Geometry and topology
One way to represent the Möbius strip as a subset of R3 is using the parametrization:
where 0 ≤ u < 2π and −1 ≤ v ≤ 1. This creates a Möbius strip of width 1 whose center circle has radius 1, lies in the xy plane and is centered at (0, 0, 0). The parameter u runs around the strip while v moves from one edge to the other.
In cylindrical polar coordinates (r, θ, z), an unbounded version of the Möbius strip can be represented by the equation:
Topologically, the Möbius strip can be defined as the square [0,1] × [0,1] with its top and bottom sides identified by the relation (x, 0) ~ (1 − x, 1) for 0 ≤ x ≤ 1, as in the diagram on the right.
A less used presentation of the Möbius strip is as the orbifold quotient of a torus.[5] A torus can be constructed as the square [0,1] × [0,1] with the edges identified as (0,y) ~ (1,y) (glue left to right) and (x,0) ~ (x,1) (glue bottom to top). If one then also identified (x,y) ~ (y,x), then one obtains the Möbius strip. The diagonal of the square (the points (x,x) where both coordinates agree) becomes the boundary of the Möbius strip, and carries an orbifold structure, which geometrically corresponds to "reflection" – geodesics (straight lines) in the Möbius strip reflect off the edge back into the strip. Notationally, this is written as T2/S2 – the 2-torus quotiented by the group action of the symmetric group on two letters (switching coordinates), and it can be thought of as the configuration space of two unordered points on the circle, possibly the same (the edge corresponds to the points being the same), with the torus corresponding to two ordered points on the circle.
The Möbius strip is a two-dimensional compact manifold (i.e. a surface) with boundary. It is a standard example of a surface which is not orientable. The Möbius strip is also a standard example used to illustrate the mathematical concept of a fiber bundle. Specifically, it is a nontrivial bundle over the circle S1 with a fiber the unit interval, I = [0,1]. Looking only at the edge of the Möbius strip gives a nontrivial two point (or Z2) bundle over S1.
A simple construction of the Möbius strip which can be used to portray it in computer graphics or modeling packages is as follows :
- Take a rectangular strip. Rotate it around a fixed point not in its plane. At every step also rotate the strip along a line in its plane (the line which divides the strip in two) and perpendicular to the main orbital radius. The surface generated on one complete revolution is the Möbius strip.
- Take a Möbius strip and cut it along the middle of the strip. This will form a new strip, which is a rectangle joined by rotating one end a whole turn. By cutting it down the middle again, this forms two interlocking whole-turn strips.
The open Möbius band
The open Möbius band is formed by deleting the boundary of the standard Möbius band. It is constructed from the set S = { (x,y) ∈ R2 : 0 ≤ x ≤ 1 and 0 < y < 1} by identifying (glueing) the points (0,y) and (1,1−y) for all 0 < y < 1.
Occurrence and use in mathematics
The space of unoriented lines in the plane is diffeomorphic to the open Möbius band.[6]
To see why, notice that each line in the plane has an equation ax + by + c = 0 for fixed constants a, b and c. We can identify the equation ax + by + c = 0 with the point (a,b,c). However, the line given by ax + by + c = 0 is also given by λ(ax + by + c) = (λa)x + (λb)y + (λc) = 0 for all λ ≠ 0.
These equations, which give the same line, are identified with the points (λa,λb,λc). Thus, the space of lines in the plane is a (proper) subset of the real projective plane; where the equation ax + by + c = 0 corresponds to the point (a:b:c) in homogeneous coordinates. It is only a subset because some equations of the form ax + by + c = 0 do not give lines. We need to disallow a = b = 0 to be sure that the equation ax + by + c = 0 does indeed give a line. The space of unoriented lines in the plane is given by deleting the point (0:0:c) = (0:0:1) from the real projective plane. This space is exactly the open Möbius band.
Möbius band with flat edge
The edge of a Möbius strip is topologically equivalent to the circle. Under the usual embeddings of the strip in Euclidean space, as above, this edge is not an ordinary (flat) circle. It is possible to embed a Möbius strip in three dimensions so that the edge is a circle. One way to think of this is to begin with a minimal Klein bottle immersed in the 3-sphere and take half of it, which is an embedded Möbius band in 4-space; this figure M has been called the "Sudanese Möbius Band". (The name comes from a combination of the names of two topologists, Sue Goodman and Daniel Asimov). Applying stereographic projection to M puts it in 3-dimensional space, as can be seen here as well as in the pictures below. (Some have incorrectly labeled the stereographic image in 3-space "Sudanese", but this is rather an image of the actual Sudanese one, which has a high degree of symmetry as a Riemannian surface: its isometry group contains SO(2). A well-known parametrization of it follows.)
To see this, first consider such an embedding into the 3-sphere S3 regarded as a subset of R4. A parametrization for this embedding is given by {(z1(η,φ), z2(η,φ))}, where
Here we have used complex notation and regarded R4 as C2. The parameter η runs from 0 to π and φ runs from 0 to 2π. Since | z1 |2 + | z2 |2 = 1 the embedded surface lies entirely on S3. The boundary of the strip is given by | z2 | = 1 (corresponding to η = 0, π), which is clearly a circle on the 3-sphere.
To obtain an embedding of the Möbius strip in R3 one maps S3 to R3 via a stereographic projection. The projection point can be any point on S3 which does not lie on the embedded Möbius strip (this rules out all the usual projection points). Stereographic projections map circles to circles and will preserve the circular boundary of the strip. The result is a smooth embedding of the Möbius strip into R3 with a circular edge and no self-intersections.
Related objects
A closely related 'strange' geometrical object is the Klein bottle. A Klein bottle can be produced by gluing two Möbius strips together along their edges; this cannot be done in ordinary three-dimensional Euclidean space without creating self-intersections.[7]
Another closely related manifold is the real projective plane. If a circular disk is cut out of the real projective plane, what is left is a Möbius strip.[8] Going in the other direction, if one glues a disk to a Möbius strip by identifying their boundaries, the result is the projective plane. In order to visualize this, it is helpful to deform the Möbius strip so that its boundary is an ordinary circle (see above). The real projective plane, like the Klein bottle, cannot be embedded in three-dimensions without self-intersections.
In graph theory, the Möbius ladder is a cubic graph closely related to the Möbius strip.
Applications
There have been several technical applications for the Möbius strip. Giant Möbius strips have been used as conveyor belts that last longer because the entire surface area of the belt gets the same amount of wear, and as continuous-loop recording tapes (to double the playing time). Möbius strips are common in the manufacture of fabric computer printer and typewriter ribbons, as they allow the ribbon to be twice as wide as the print head while using both half-edges evenly.
A device called a Möbius resistor is an electronic circuit element that has the property of canceling its own inductive reactance. Nikola Tesla patented similar technology in the early 1900s:[9] "Coil for Electro Magnets" was intended for use with his system of global transmission of electricity without wires.
The Möbius strip is the configuration space of two unordered points on a circle. Consequently, in music theory, the space of all two note chords, known as dyads, takes the shape of a Möbius strip; this and generalizations to more points is a significant application of orbifolds to music theory.[10][11]
In physics/electro-technology:
- as compact resonator with the resonance frequency which is half that of identically constructed linear coils[12]
- as inductionless resistance[13]
- as superconductors with high transition temperature[14]
In chemistry/nano-technology:
- as molecular knots with special characteristics (Knotane [2], Chirality)
- as molecular engines[15]
- as graphene volume (nano-graphite) with new electronic characteristics, like helical magnetism[16]
- in a special type of aromaticity: Möbius aromaticity
- charged particles, which were caught in the magnetic field of the earth, can move on a Möbius band[17]
- the cyclotide (cyclic protein) Kalata B1, active substance of the plant Oldenlandia affinis, contains Möbius topology for the peptide backbone.
See also
References
- ^ Clifford A. Pickover (March 2006). The Möbius Strip : Dr. August Möbius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. Thunder's Mouth Press. ISBN 1560258268.
- ^ Rainer Herges (2005). Möbius, Escher, Bach – Das unendliche Band in Kunst und Wissenschaft . In: Naturwissenschaftliche Rundschau 6/58/2005. pp. 301–310. ISSN 0028-1050.
- ^ Chris Rodley (ed.) (1997). Lynch on Lynch. London, Boston. pp. 231.
- ^ Starostin E.L., van der Heijden G.H.M. (2007). "The shape of a Möbius strip". Nature Materials 6 (8): 563–7. doi:10.1038/nmat1929. PMID 17632519. http://www.nature.com/nmat/journal/v6/n8/abs/nmat1929.html.
- ^ Tony Phillips, Tony Phillips' Take on Math in the Media, American Mathematical Society, October 2006
- ^ Parker, Phillip (1993). "Spaces of Geodesics". Aportaciones Matemáticas. Notas de Investigación (UASLP): 67 − 79. http://www.math.wichita.edu/~pparker/research/sog.htm.
- ^ Spivak, Michael (1979). A Comprehensive Introduction to Differential Geometry, Volume I (2nd ed.). Wilmington, Delaware: Publish or Perish. pp. 591.
- ^ Hilbert, David; S. Cohn-Vossen (1999). Geometry and the Imagination (2nd ed.). Providence, Rhode Island: American Mathematical Society. pp. 316. ISBN 9780821819982.
- ^ U.S. Patent 512,340
- ^ Clara Moskowitz, Music Reduced to Beautiful Math, LiveScience
- ^ Dmitri Tymoczko (7 July 2006). "The Geometry of Musical Chords". Science 313 (5783): 72–4. doi:10.1126/science.1126287. PMID 16825563.
- ^ IEEE of Trans. Microwave Theory and Tech., volume. 48, No. 12, pp. 2465–2471, Dec. 2000
- ^ U.S. Patent 3.267.406
- ^ Enriquez, Raul Perez (2002). "A Structural parameter for High Tc Superconductivity from an Octahedral Moebius Strip in RBaCuO: 123 type of perovskite". Rev Mex Fis 48 (supplement 1): 262. arXiv:cond-mat/0308019.
- ^ Angew Chem Int OD English one 2005 February 25; 44 (10): 1456–77.
- ^ Yamashiro, Atsushi; Shimoi, Yukihiro; Harigaya, Kikuo; Wakabayashi, Katsunori (2004). "Novel Electronic States in Graphene Ribbons -Competing Spin and Charge Orders-". Physica E 22 (1–3): 688–691. arXiv:cond-mat/0309636. doi:10.1016/j.physe.2003.12.100.
- ^ IEEE Transactions on plasma Science, volume. 30, No. 1, February 2002
External links
- Möbius Strip Video
- A virtual walk in the solar wind
- Animation of a rotating Sudanese Möbius band
- Louis Buckley (2007-07-15). "Möbius strip unravelled". Nature. doi:10.1038/news070709-16. http://www.nature.com/news/2007/070709/full/070709-16.html. Retrieved 2006-07-16.
- h2g2 - The Amazing Möbius Strip
- Johann Benedict Listing
- Knitted version
- Möbius Strip Music Box
- Möbius strip at cut-the-knot
- Science News 7/28/07: A Twist on the Möbius Band: Researchers work out the shape of a paper strip
- The Möbius Gear — A functional planetary gear model in which one gear is a Möbius strip
- Visualization of J. S. Bach's crab canon on a Möbius strip
- The protein with a topological twist
- Tridimensional and rotational möbius strip
- Weisstein, Eric W., "Möbius Strip" from MathWorld.
- Huckel spectra of Mobius pi systems
- Beyond the Mobius Strip